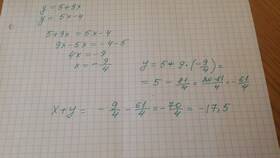Сумма функций - это операция, широко применяемая в математическом анализе, алгебре и прикладных науках. Рассмотрим основные методы нахождения суммы функций и их свойства.
Содержание
Определение суммы функций
Суммой двух функций f(x) и g(x) называется функция h(x) = f(x) + g(x), определенная на пересечении областей определения исходных функций.
Основные методы нахождения суммы
| Метод | Описание |
| Алгебраическое сложение | Непосредственное сложение выражений функций |
| Графический метод | Построение графиков и их поточечное сложение |
| Численные методы | Вычисление значений в точках и их суммирование |
Алгебраическое сложение функций
- Определите области определения обеих функций
- Найдите пересечение областей определения
- Запишите выражение для суммы функций
- Упростите полученное выражение (если возможно)
- Определите свойства результирующей функции
Примеры сложения функций
Линейные функции
f(x) = 2x + 3
g(x) = x - 5
(f + g)(x) = 3x - 2
Тригонометрические функции
f(x) = sin(x)
g(x) = cos(x)
(f + g)(x) = sin(x) + cos(x)
Свойства суммы функций
- Коммутативность: f + g = g + f
- Ассоциативность: (f + g) + h = f + (g + h)
- Нейтральный элемент: f + 0 = f (где 0 - нулевая функция)
- Дистрибутивность относительно умножения на скаляр: a(f + g) = af + ag
Особые случаи
| Тип функций | Особенности сложения |
| Ортогональные | Норма суммы равна корню из суммы квадратов норм |
| Периодические | Период суммы - НОК периодов слагаемых |
| Комплексные | Складываются отдельно действительные и мнимые части |
Применение в математическом анализе
- Разложение функций в ряды
- Решение дифференциальных уравнений
- Гармонический анализ
- Аппроксимация функций
Численные методы сложения
- Выберите набор точек xi в области определения
- Вычислите значения f(xi) и g(xi)
- Найдите h(xi) = f(xi) + g(xi)
- Постройте таблицу или график результирующей функции
Частые ошибки
- Сложение функций с непересекающимися областями определения
- Неучет особенностей слагаемых (разрывы, асимптоты)
- Неправильное упрощение сложных выражений
- Путаница между суммой функций и композицией
0. Практические советы
- Всегда проверяйте области определения
- Анализируйте поведение суммы на границах области
- Используйте компьютерные системы для сложных вычислений
- Проверяйте результат на контрольных точках
Нахождение суммы функций - фундаментальная операция в математике, имеющая широкое применение в различных областях науки и техники. Правильное применение методов сложения функций позволяет решать сложные задачи и анализировать поведение систем.