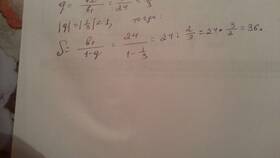Геометрическая прогрессия - это последовательность чисел, где каждое последующее число получается умножением предыдущего на постоянное число (знаменатель прогрессии). Рассмотрим методы вычисления суммы членов такой прогрессии.
Содержание
Формула суммы геометрической прогрессии
Для конечной геометрической прогрессии с первым членом b₁, знаменателем q и количеством членов n сумма вычисляется по формуле:
Sₙ = b₁(1 - qⁿ)/(1 - q), при q ≠ 1
Шаги вычисления суммы
- Определите первый член прогрессии (b₁)
- Найдите знаменатель прогрессии (q)
- Установите количество членов (n)
- Подставьте значения в формулу
- Выполните вычисления
Частные случаи
| Условие | Формула |
| |q| < 1 и n → ∞ | S = b₁/(1 - q) |
| q = 1 | Sₙ = n·b₁ |
| q = -1 и n четное | Sₙ = 0 |
Пример расчета
Дана прогрессия: 2, 6, 18, 54 (n=4)
- b₁ = 2
- q = 3 (6/2 = 3)
- n = 4
- S₄ = 2(1 - 3⁴)/(1 - 3) = 2(1 - 81)/(-2) = 80
Практическое применение
- Расчет сложных процентов в финансах
- Моделирование биологических популяций
- Анализ алгоритмов в информатике
- Решение физических задач о цепных реакциях
Проверка правильности вычислений
- Убедитесь, что последовательность действительно геометрическая
- Проверьте правильность определения знаменателя
- Для бесконечной прогрессии убедитесь, что |q| < 1
- Сравните результат с последовательным сложением членов
Графическое представление
При |q| < 1 сумма бесконечной прогрессии стремится к конечному значению, что можно наблюдать на графике в виде приближения к горизонтальной асимптоте.
Понимание принципов вычисления суммы геометрической прогрессии важно для решения широкого круга математических и прикладных задач. Правильное применение формул позволяет значительно упростить расчеты.